CROISSANCE ÉCONOMIQUE

CROISSANCE ÉCONOMIQUE

En biologie, la notion de croissance évoque l’idée d’un développement progressif et organique. Par analogie, le même terme sert à définir un ensemble de phénomènes économiques. La définition doit en être formulée à deux points de vue. D’un point de vue statistique d’abord, théorique ensuite.

Le repérage statistique des phénomènes de croissance économique permet de poser les problèmes auxquels la théorie de la croissance cherche à apporter une solution, mais il ne peut prétendre les résoudre. L’explication des raisons de la croissance d’une économie, de ses variations de vitesse, du taux plus ou moins élevé qui la caractérise par rapport à d’autres économies nationales repose sur un ensemble d’hypothèses. Leur formulation permet notamment la construction de modèles théoriques. La théorie postkeynésienne, la théorie néoclassique de la croissance – auxquelles appartiennent les modèles postkeynésiens et néo-classiques dont il sera essentiellement question ci-dessous – constituent, avec la théorie marxiste de l’accumulation du capital (cf. CAPITALISME, DÉPRESSION ÉCONOMIQUE, MARX ET MARXISME), les principaux courants de la pensée économique en matière de croissance.

1. La notion

Repérage statistique

D’un point de vue statistique, la croissance peut se définir comme un mode de comportement de certaines grandeurs économiques en fonction du temps. L’évolution des grandeurs observées au cours du temps est ainsi caractérisée par un mouvement systématique de caractère monotonique suffisamment régulier sur une durée suffisamment longue pour permettre un ajustement des séries chronologiques sur un trend , c’est-à-dire sur la représentation mathématique d’une tendance. La croissance apparaît donc comme un mouvement de longue durée, au moins par rapport aux variations dans le rythme de l’évolution qui, sous la forme de phénomènes d’accélération ou de phénomènes de décélération affectent de façon plus momentanée l’allure de l’évolution observée à partir de séries chronologiques brutes avant tout ajustement.

De ce premier point de vue, la croissance correspond à l’idée d’un progrès mesurable. La croissance peut impliquer des transformations qualitatives, mais seuls les éléments quantifiables en sont retenus. Cette démarche peut n’être que préalable; elle est nécessaire pour déterminer l’allure du phénomène et notamment sa régularité, encore qu’elle ne puisse en établir la signification. Elle a l’avantage de permettre un repérage quantitatif du développement au moyen de grandeurs considérées comme les indicateurs de la croissance: le produit intérieur brut et le produit par tête en particulier.

Parmi les allures de la croissance, l’une d’entre elles est généralement privilégiée: celle qui correspond à l’accroissement d’une grandeur Y en fonction du temps suivant une loi exponentielle, à un taux constant p , tel que: Y^t = A e ^pt . En retenant pour unité de temps la période annuelle, le produit national brut d’une année, n + 1, sera exprimé par le produit national brut de l’année précédente, n , multiplié dans une proportion constante (1 + p ), de telle sorte que: Y^t = Y⁰ (1 + p )^t . La plupart des grandeurs retenues comme indicateurs de la croissance progressent suivant des taux relatifs d’accroissement, p = Y/Y, de l’ordre de 1 à 10 p. 100 par an, suivant des périodes de doublement de la valeur de la grandeur observée se situant entre 70 ans et 7 ans. En passant du «temps discret», c’est-à-dire fractionné en périodes, au «temps continu», le taux p peut s’écrire sous la forme différentielle: p = (1/Y) (d Y/dt ), qui est la forme sous laquelle il apparaît généralement dans les modèles de croissance étudiés plus loin.

Historiquement, la croissance du produit national, réévalué à prix constants, s’est effectuée dans les pays occidentaux à des taux variables suivant les époques et suivant les économies (tabl. 1). Généralement rapide dans la période 1850-1873, elle se ralentit par la suite, la période 1882-1896 étant notamment une phase de stagnation pour l’économie française. Celle qui va de 1897 à la Première Guerre mondiale est au contraire une période de croissance très rapide à l’échelle internationale. La grande dépression des années qui suivent 1929 est un phénomène cyclique, certes, mais qui semble associé à un freinage durable de la croissance. La période des Trente Glorieuses, qui va de la reconstruction après la Seconde Guerre mondiale au premier choc pétrolier, a montré au contraire une croissance rapide, notamment jusqu’en 1968.

Il faut néanmoins se garder d’exagérer la portée des différences constatées dans les taux suivant les époques ou suivant les pays. Elles tiennent pour partie à l’incertitude des données statistiques (notamment celles qui sont nécessaires à la réévaluation des données à prix courants en données à prix constants), qui est de plus en plus grande à mesure que l’on remonte dans le temps. Elles tiennent aussi au caractère relativement arbitraire des années limites choisies pour le calcul des taux constants d’accroissement en moyenne géométrique annuelle: l’incertitude pèse sur les points d’inflexion des séries chronologiques, nées non seulement des perturbations de l’activité économique provenant des mouvements cycliques, mais aussi d’accidents majeurs, comme les guerres.

Alors que la décennie 1950-1959 a été souvent considérée comme une période de croissance exceptionnelle, la comparaison avec la période 1922-1929 montre que des taux aussi élevés ne sont pas sans précédent, à condition de prendre dans la comparaison un échantillon de pays suffisamment large (tabl. 2). On doit également admettre qu’à mesure que l’on étend la période d’observation, des différences dans les taux de croissance entre pays, qui semblaient considérables lorsque ces taux étaient calculés sur des périodes relativement brèves, tendent à s’atténuer, voire à disparaître. Dans la période 1950-1960, la croissance aux États-Unis a été relativement lente si on la compare à celle des pays d’Europe occidentale; la différence s’atténue si on calcule les taux sur l’ensemble de la période d’après-guerre jusqu’au début des années soixante-dix.

Ces réserves faites, il faut admettre qu’il existe des différences considérables entre les taux de croissance de pays tels que le Japon (croissance exceptionnellement rapide), l’Allemagne fédérale (croissance rapide) et la Grande-Bretagne (croissance lente), même si on les calcule sur une longue période.

Recherche des causes

D’un point de vue théorique, les lois mathématiques du mouvement ne sont que le point de départ d’une définition de la croissance en tant que processus. Par analogie avec la notion biologique de croissance, la croissance économique ne saurait se réduire à l’accroissement continu et régulier d’une seule grandeur économique. La prise en considération d’un phénomène de ce genre peut fournir un indicateur de la croissance; elle ne donne en soi aucune explication quant aux causes du mouvement.

Celles-ci doivent être recherchées en prenant en considération les interrelations qui, au cours du temps, s’établissent entre différentes grandeurs en voie d’accroissement. Sans aller jusqu’à élaborer une explication englobante d’un système économique et de ses transformations, ce qui est du domaine de la théorie du développement, la théorie de la croissance a pour objet d’expliquer le processus de caractère cumulatif et, en quelque sorte, d’auto-entraînement, par lequel les grandeurs globales ou semi-globales caractéristiques d’un système, et dont les valeurs se conditionnent les unes aux autres en chaque point du temps, agissent les unes sur les autres de façon continue pour provoquer leur expansion réciproque au cours du temps.

La théorie de la croissance pose de façon distincte, mais intimement liée, deux problèmes fondamentaux: celui des sources et des facteurs de la croissance; celui de l’équilibre d’un système économique en voie de croissance, dont dépendent la continuité et la régularité du mouvement. Compte tenu du caractère non seulement auto-entretenu, mais autogène du mouvement de croissance, qui est supposé s’engendrer de lui-même lorsque certaines conditions sont remplies, les deux problèmes doivent être traités conjointement. La théorie de la croissance apparaît ainsi comme une branche de la théorie dynamique des équilibres macro-économiques (c’est-à-dire des équilibres entre grandeurs globales). La détermination d’un état d’équilibre et des conditions de sa stabilité y est abordée à partir de considérations relatives, non pas aux niveaux des grandeurs et de leurs ajustements réciproques, mais aux taux de variation de ces grandeurs. Non seulement le problème de la compatibilité des variations entre elles est ainsi posé, mais la théorie est amenée à privilégier certaines interrelations entre les phénomènes comme ayant un caractère moteur; ce qui permet de distinguer la théorie de la croissance et une théorie telle que celle des équilibres de marchés, en statique, où les grandeurs entrant en relation d’interdépendance sont considérées comme exerçant les unes sur les autres des influences réciproques de caractère réversible. Ces considérations permettent également de distinguer la théorie de la croissance et d’autres analyses dynamiques, telles que certaines théories des mouvements cycliques où les raisons du mouvement se trouvent dans le caractère anticipé ou retardé de la réaction d’une grandeur à la variation d’une autre, le caractère de réciprocité des interdépendances n’étant altéré que du fait de l’absence de simultanéité des actions et des réactions.

La théorie de la croissance ainsi entendue s’est développée depuis les années cinquante, de façon tardive par rapport à d’autres branches de l’analyse économique. Son développement a été rapide et a donné lieu à l’élaboration d’un très grand nombre de modèles. Tous ont en commun de rechercher l’explication de la croissance dans les relations entre le produit, les facteurs de production (en ne retenant généralement que le capital et le travail) et la productivité des facteurs entrant en combinaison, ce qui amène à introduire des considérations relatives au progrès technique.

Les modèles

Suivant les hypothèses faites au point de départ quant aux lois régissant la mise en combinaison des facteurs de production (complémentarité ou substituabilité des facteurs), on peut distinguer deux familles de modèles. Sous-jacentes à cette classification des modèles, des options théoriques antagonistes sont en cause: celle des disciples et continuateurs de Keynes; celle des économistes néo-classiques. À partir du choix d’une hypothèse de complémentarité des facteurs dans un cas, de substituabilité dans l’autre, seront étudiées successivement la théorie postkeynésienne et la théorie néo-classique de la croissance qui, avec la théorie marxiste de l’accumulation du capital (qui a trait à la fois aux mouvements cycliques, à la croissance et à l’évolution du système capitaliste), constituent les courants dominants de la pensée théorique dans cette matière.

Le point de départ des modèles de croissance réside dans la notion de fonction de production, c’est-à-dire d’une relation fonctionnelle existant entre les facteurs mis en œuvre, à savoir le stock de capital K et le travail L, considéré également comme un potentiel de production dont l’évaluation sera précisée plus loin, et, d’autre part, le flux du produit obtenu (P) en mettant en œuvre des facteurs de production, soit:

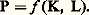Pour une période de temps unitaire, le flux du produit final sera déterminé par les valeurs ajoutées dues à l’usage du capital et à l’emploi du travail pendant la même période.

Étant admis qu’en chaque point du temps il est fait un emploi rationnel des facteurs disponibles, de façon à minimiser les coûts de facteurs relativement au résultat obtenu, le taux de croissance du produit P, pendant une période de temps déterminée, dépendra des dotations initiales en facteurs de l’économie considérée et de leurs taux de croissance pendant la même période.

À partir de ce point de départ commun, les modèles diffèrent suivant la façon dont on conçoit les contraintes qui délimitent les possibilités de distribution rationnelle des facteurs, en définissant les techniques de production par les proportions entre lesquelles les facteurs entrent en combinaison.

Dans l’hypothèse la plus contraignante, qui est celle de la complémentarité, on supposera qu’il existe une seule technique de production, définie par un rapport K/L constant, pour l’obtention de chaque produit, ou encore, si le produit est homogène (ce qu’il faut supposer pour simplifier), qu’il existe une technique unique. Dans ce cas, le plein emploi d’un facteur entraîne, de façon rigide, le plein emploi de l’autre. Réciproquement, employer plus d’un facteur, sans accroître dans la même proportion l’emploi de l’autre, n’aboutit à aucun accroissement du produit. La fonction de production pour une valeur de P donnée n’admet qu’une valeur de K et de L.

À l’inverse, dans l’hypothèse de substituabilité, la fonction de production est continue. Un produit P, d’une valeur donnée, peut être obtenu au moyen d’un très grand nombre de techniques alternatives et, théoriquement, on considère qu’il est possible de faire varier continûment le rapport K/L. Une technique sera effectivement choisie, mais la valeur de K/L correspondante ne peut être déterminée qu’en introduisant une nouvelle contrainte: le rapport existant au même moment entre les coûts unitaires ou entre les prix des facteurs. Il reste toujours possible d’obtenir une même valeur du produit P à partir d’une technique de production différente, et, de fait, le rapport K/L se modifie si change le rapport entre les prix des facteurs, c’est-à-dire entre le coût unitaire en capital et le taux de salaire unitaire.

Cette seconde hypothèse peut paraître également extrême. Elle peut être modérée si l’on suppose que la fonction de production est continue: on suppose alors qu’il existe un nombre fini, voire restreint, de techniques de production. Cette hypothèse, qui n’a été utilisée que récemment dans la construction de modèles de croissance purement théoriques, est celle sur laquelle repose la programmation linéaire, méthode couramment employée en matière de planification.

Seuls seront étudiés ici les modèles post-keynésiens et néo-classiques, fondés respectivement sur l’hypothèse soit d’une complète rigidité, soit d’une complète flexibilité du rapport K/L. Dans le second cas, une hypothèse supplémentaire devra être faite en ce qui concerne la valeur du coefficient d’élasticité de substitution entre facteurs, c’est-à-dire d’un coefficient mesurant la plus ou moins grande facilité avec laquelle il est possible de remplacer un facteur par l’autre à un niveau de production donné.

De cette façon, l’hypothèse de la plasticité des techniques de production se trouve précisée: plus faible est l’élasticité de substitution, moindre est, toutes choses égales d’ailleurs, la flexibilité du rapport K/L en réponse à une variation unitaire du rapport des prix des facteurs. À la limite, une élasticité de substitution nulle implique une complète rigidité du rapport K/L et fait de la complémentarité un cas particulier de la substituabilité. Notons enfin que l’hypothèse de substituabilité peut être aménagée dans un sens restrictif au moyen d’un certain nombre de distinctions. (La substituabilité peut être interprétée par exemple comme jouant seulement ex ante dans le choix des techniques de production, mais non ex post pour l’utilisation des facteurs de production déjà produits dans des emplois dont il est exclu qu’ils soient alternatifs, compte tenu de leur caractère spécifique: qualification professionnelle de la main-d’œuvre, absence de malléabilité du capital.)

2. Les modèles postkeynésiens

L’hypothèse

L’hypothèse de complémentarité permet de faire éclater la fonction de production en deux relations distinctes: les rapports entre les facteurs et la production peuvent être approchés de façon unilatérale, soit sous la forme P = P(K), soit sous la forme P = P(L).

Il convient d’aborder l’exposé des modèles de ce genre à partir de la relation entre le capital et le produit, ces modèles ayant surtout eu pour but d’expliquer ou de planifier la croissance à partir de la formation du capital, considéré comme l’élément moteur dans tout processus de croissance. L’hypothèse de complémentarité impliquant que le travail soit disponible, en quantité ou en qualité productive dans la proportion voulue pour produire le volume de production déterminé suivant la relation capital-produit, amène à étudier les relations entre le produit, le travail et le progrès technique. Le modèle ainsi construit permet d’atteindre un certain nombre de conclusions en ce qui concerne le jeu des facteurs déterminant la croissance et, plus encore, de formuler de façon contraignante les conditions auxquelles un processus de croissance peut se dérouler de façon équilibrée.

Capital et croissance

Le capital joue un rôle privilégié dans l’explication de la croissance. Il est à la fois produit et facteur de production. Le capital est en relation avec la production à la fois à titre de conséquence du point de vue de son offre, c’est-à-dire de l’épargne, et à titre de cause du point de vue de la demande qui en est faite aux fins d’investissement: l’épargne sert à financer les dépenses ayant pour objet d’accroître le stock de capital et, par là, la capacité de production.

Les auteurs de l’école postkeynésienne (E. D. Domar, R. Harrod...) interprètent de façon dynamique la condition d’équilibre des grandeurs globales (I = S) formulée dans la théorie générale de Keynes. Ce dernier la concevait dans le cadre d’un raisonnement monétaire et a-temporel en tant que l’équivalence entre le montant d’épargne S et le montant d’investissement I. Ces auteurs l’interprètent comme l’équivalence nécessaire au cours du temps entre le taux d’épargne s , entendu au sens de la proportion (s = S/P) dans laquelle un prélèvement est opéré sur le produit réel au moyen de l’épargne en vue de financer la formation du capital, d’une part, et le taux d’investissement (i = I/P) correspondant aux dépenses de formation du capital en proportion de l’ensemble des dépenses correspondant à la production globale, d’autre part.

Au montant des dépenses d’investissement considérées nettes par unité de temps correspond l’accroissement du stock de capital, K⁰, autrement dit l’investissement exprime la vitesse à laquelle s’accroît le capital. La relation d’équivalence entre l’épargne et l’investissement peut donc s’écrire sous forme d’une équation d’offre du capital:

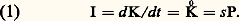L’équation de demande du capital s’écrira sous la forme:

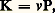dans laquelle v est un paramètre dit «coefficient de capital», dont la fixité supposée est en accord avec l’hypothèse faite quant à la complémentarité des facteurs.

La fonction de production est ici une relation linéaire et homogène, compte tenu de l’absence supposée d’économies d’échelle, c’est-à-dire de l’absence de toute variation favorable de P relativement à K lorsque l’on produit à plus grande échelle par suite d’une meilleure utilisation du capital, liée à la dimension à laquelle on produit. Cette relation se réduit à un coefficient de proportionnalité fixe de K par rapport à P, le rapport inverse, P/K, exprimant la productivité unitaire du capital, étant lui-même constant.

Le coefficient de capital exprime l’accroissement du capital nécessaire en proportion de l’accroissement du produit recherché, qui correspond au montant de l’investissement qui doit être entrepris pour obtenir l’accroissement du produit, et à la même valeur que le coefficient moyen v ; aussi, à la marge, peut-on écrire:

À partir des équations (1) et (2), le taux de croissance du produit p , soit P⁰/P = (1/P) (d P/dt ), est déterminé:

Un exemple numérique simple peut aider à comprendre le raisonnement. L’équivalence entre les taux s et i (c’est-à-dire: S/P = I/P) peut s’énoncer ainsi: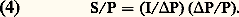

En raisonnant sur une courte période de temps au début de laquelle le stock de capital est égal à 300, l’équation (4) pouvant s’écrire sous la forme: s = vp en supposant v = 3 et s = 15/100, le taux d’accroissement du produit sera: p = 5/100, c’est-à-dire un taux de 5 p. 100 résultant d’une proportion de l’épargne dans le produit égale à 15 p. 100, divisée par un coefficient de capital v, égal à 3; ou encore un taux d’épargne de 15 p. 100 multiplié par l’inverse du coefficient de capital (1/v = P/K), 1/v exprimant le taux constant de productivité moyenne unitaire du capital, ici égal à 0,33. Par ailleurs, le capital se sera accru pendant la période à un taux I/K, soit donc 15/300, c’est-à-dire à un taux k égal au taux p d’accroissement du produit.

Un certain nombre de conclusions peuvent alors être dégagées quant au rôle que joue la formation du capital dans la croissance du produit, abstraction faite du rôle complémentaire que le travail et le progrès technique joueront. En premier lieu, le taux k et le taux p auxquels le capital et le produit s’accroissent respectivement doivent être équivalents, cela étant impliqué par la constance du coefficient de capital. En second lieu, le taux de croissance du produit, p = s/v , pour une valeur donnée du coefficient de capital v , est directement proportionnel au taux d’épargne. Plus importante est la formation du capital en proportion du produit, plus rapide est la croissance du produit.

Cette conclusion, affirmant la primauté du capital comme facteur de croissance, est, d’un point de vue théorique, subordonnée à l’hypothèse que la valeur de v est donnée indépendamment de celle de s , ce qui est remis en cause par les modèles néo-classiques (cf. chap. 3). D’un point de vue statistique, la même conclusion est subordonnée à l’observation d’une constance de la valeur de v .

Pour une même économie, les calculs du coefficient de capital montrent généralement une tendance à la stabilité, sous réserve d’oscillations lentes autour d’une valeur moyenne, encore que la stabilité apparente de v puisse être le résultat de la neutralisation de forces jouant en sens opposés sur sa valeur, comme s’efforcent de le montrer les modèles néo-classiques (cf. chap. 3).

En revanche, l’observation montre que, d’un pays à un autre, sur une même période de temps, la valeur de v peut varier du simple au triple (tabl. 3). Dans ce cas, l’explication des différences de taux de croissance du produit de pays à pays doit faire intervenir tout à la fois la valeur de s et la valeur de v . Par exemple, dans la décennie 1950-1960, l’Allemagne fédérale a obtenu un taux de croissance du produit élevé, qui s’explique par la conjugaison d’un taux d’investissement élevé et d’un coefficient de capital favorable, c’est-à-dire de valeur faible. Malgré un effort d’investissement non moins remarquable, la Norvège n’a obtenu, en comparaison, qu’un taux de croissance faible, compte tenu du caractère anormalement élevé de son coefficient de capital. La France, en dépit d’un taux d’investissement moindre, a obtenu un taux de croissance satisfaisant, compte tenu de la valeur favorable du coefficient de capital. La Grande-Bretagne n’a obtenu qu’un taux de croissance faible, conséquence de la conjugaison d’un taux d’investissement faible et d’un coefficient de capital élevé (tabl. 4).

Travail et croissance

Dans des modèles de ce genre, le travail étant en rapport de complémentarité avec le capital, la détermination du produit à partir de sa relation avec le travail, P = P(L), doit concorder avec la détermination précédente, P = P(K), faute de quoi le processus de croissance serait déséquilibré et dégénérerait soit en chômage, soit en inflation.

Là encore, le problème doit être abordé à la fois du point de vue de l’offre et de celui de la demande du facteur travail. On peut remarquer que cette offre et cette demande du facteur travail, noté jusqu’à présent L, doivent être appréciées en tant que potentiel de production en tenant compte de la quantité de travail disponible N, mesurée en nombre d’heures (ou au moyen d’indices de la population active, du taux d’activité, etc.), et de son niveau d’efficience A. En effet, une heure de travail à un niveau d’efficience double vaut autant en capacité productive que deux heures de travail à un niveau d’efficience simple, de telle sorte que L = A 練 N.

Considérons en premier lieu l’offre et la demande de travail en tant que quantités du facteur N, abstraction faite des effets que le progrès technique peut exercer sur la productivité du travail.

Par rapport au capital, l’offre de travail varie de façon exogène en fonction de facteurs démographiques. Considérons l’hypothèse où, en conséquence de ces facteurs, la population active s’accroît de façon régulière à un taux constant n . Ce taux est généralement, dans les pays développés du moins, nettement inférieur au taux d’accroissement du produit. En reprenant l’exemple numérique précédent, où p = 5 p. 100, nous supposerons que n = 2 p. 100. Apparemment, le taux p prévu ne pourra être obtenu, faute d’une croissance suffisante de la force de travail. Néanmoins, jusqu’à ce point du raisonnement, en assimilant L à N on a négligé l’effet éventuel d’une amélioration de la productivité de la main-d’œuvre.

Il est possible d’en tenir compte indirectement en prenant en considération le coefficient d’élasticité à long terme de la demande de main-d’œuvre par rapport à la production. En supposant que cette élasticité est constante, l’équation de la demande de travail s’écrit:

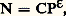C étant une constante et 﨎 étant la valeur du coefficient d’élasticité en question (coefficient de Verdorn) qui mesure la proportion dans laquelle une variation de N entraîne une variation de la demande de travail (lg N = 﨎 lg P).

Le taux de croissance du produit déterminé à partir du potentiel de production que constitue le travail sera:

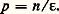Si nous supposons que la valeur de 﨎 est égale à 0,4, pour un taux de croissance de la quantité de travail disponible n = 2 p. 100, le taux de croissance du produit p sera de 5 p. 100, c’est-à-dire que, dans ce cas, la détermination du taux de croissance à partir du capital et sa détermination à partir du travail coïncideront.

Les calculs faits sur la valeur de 﨎 montrent qu’effectivement celle-ci est nettement inférieure à l’unité. Cela revient à dire que, abstraction faite des influences cycliques ou momentanées qui peuvent s’exercer sur l’élacticité de la demande de travail par rapport à la production, l’accroissement de la production demande un accroissement moins que proportionnel du nombre des heures de travail fournies dans les mêmes unités de temps.

Progrès technique et croissance

Cette constatation donne à penser qu’il se produit au cours du temps une amélioration à taux constant de la productivité de la main-d’œuvre; celle-ci peut compenser l’insuffisance de n relativement à p . Cela amène à prendre en considération le progrès technique et ses effets sur la productivité.

Dans tous les cas où n 麗 p , p étant déterminé par les équations d’offre et de demande du capital, la productivité du travail doit s’accroître à un taux a tel que: n + a = p . Dans l’exemple numérique sur lequel nous avons raisonné précédemment, le progrès technique doit avoir pour effet d’accroître la productivité du travail à un taux de 3 p. 100 pour que le taux d’équilibre de la croissance du produit (p = 5 p. 100), que nous avons établi précédemment à partir des rapports entre le capital et le produit, soit vérifié.

Cela implique un certain nombre d’hypothèses quant à la forme et aux effets du progrès technique. Il bénéficie intégralement à la main-d’œuvre, dont la productivité moyenne par heure de travail P/N s’accroît régulièrement (dans l’hypothèse où n 麗 p ). La productivité du capital P/K, reste en revanche constante. Dans ces conditions, le coefficient d’intensité capitalistique est croissant si on le mesure comme étant le rapport K/N, c’est-à-dire le capital employé par heure de travail. Mais si on le mesure comme étant K/L, compte tenu de l’élévation régulière du niveau de productivité de la main-d’œuvre au taux a , ce rapport reste inchangé. Toute situation où le progrès technique ne serait pas neutre en ce sens qu’il aboutirait à faire varier le rapport K/L (neutralité du progrès technique dite «au sens de Harrod» dans la littérature économique), remettrait en question les hypothèses à la base du modèle, à savoir l’invariance des techniques de production et la complémentarité des facteurs.

Stabilité de l’état de croissance

La condition la plus générale d’équilibre de la croissance, impliquant l’ensemble des relations entre le produit, le capital, le travail et le progrès technique, peut être présentée sous la forme:

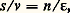dont dépend l’équivalence du taux p déterminé à partir du capital et du même taux déterminé à partir du travail.

Cela pose de façon aiguë le problème de la stabilité de l’état de croissance. En effet, les valeurs des quatre paramètres, s, v, n et 﨎 sont indépendantes les unes des autres, au moins dans les hypothèses autres que celles d’une étude de très longue période (où, par exemple, un accroissement de la population à taux n trop élevé peut entraîner une diminution du taux d’épargne s ).

Du point de vue de la planification et de la politique économique, toute action sur v étant par hypothèse exclue, la possibilité d’établir un régime permanent de croissance équilibrée dépendra de la mesure dans laquelle il est possible d’agir sur les valeurs des autres paramètres. Du point de vue de la théorie pure, les modèles de croissance de ce genre trouvent leur prolongement dans des modèles du mouvement cyclique (Domar, Harrod, Hicks), où les fluctuations cycliques apparaissent comme la conséquence quasi nécessaire de l’impossibilité de maintenir le processus de croissance sur la ligne de tendance que définissent les modèles de la croissance équilibrée.

Il n’est pas surprenant que les modèles postkeynésiens aboutissent à des conclusions pessimistes quant à la stabilité du processus de croissance, compte tenu des hypothèses contraignantes que l’on s’est données au point de départ. Les modèles élaborés par l’école néo-classique, à partir d’hypothèses moins contraignantes, illustrent une vision différente des rapports entre le produit et les facteurs et supposent une plus grande flexi-bilité des conditions d’équilibre de la croissance.

3. Les modèles néo-classiques

L’hypothèse

Les modèles néo-classiques reposent sur les fonctions de production à facteurs substituables qui prennent en considération directement le rapport entre, d’une part, le produit et, d’autre part, l’ensemble des facteurs qui peuvent être employés en proportions variables. En raisonnant sur une fonction de production à deux facteurs K et N, et en évitant provisoirement d’introduire les considérations relatives au progrès technique, la fonction de production peut s’écrire:

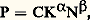où C est une constante et 見 et 廓 sont des coefficients numériques qui expriment l’élasticité de la production par rapport aux facteurs. On raisonnera selon l’hypothèse d’une fonction de production, dite fonction de Cobb-Douglas, du nom des auteurs qui, les premiers, l’ont proposée (pour expliquer les lois de détermination de la répartition du produit entre les facteurs).

La fonction de Cobb-Douglas

Une première caractéristique de cette fonction est que les exposants non seulement sont constants, mais de somme égale à l’unité:

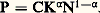L’élasticité de substitution entre facteurs y a une valeur unitaire. Par là la fonction Cobb-Douglas apparaît comme un cas particulier.

Des tentatives ont été faites pour utiliser une fonction dite C.E.S., où le coefficient mesurant l’élasticité de substitution est constant, mais peut avoir des valeurs autres que la valeur unitaire (Solow, Minhas, Arrow et Chenery). Cependant l’élasticité de substitution semble avoir généralement des valeurs proches de l’unité, et plutôt inférieures. La facilité avec laquelle (surtout sur une courte période de temps) des machines peuvent être substituées au travail humain, et vice versa, est forcément limitée. Par ailleurs, une élasticité de substitution unitaire signifie que, lorsqu’augmente de 1 p. 100 le prix d’un facteur relativement à l’autre, la quantité employée du facteur devenu plus coûteux diminue relativement à l’autre dans la même proportion, de telle sorte que la part de chaque facteur dans la répartition du produit national mesuré en valeurs ajoutées reste constante. La stabilité constatée des parts respectives du travail et du capital dans la répartition (calculée, il est vrai, sous réserve d’une ventilation assez arbitraire des revenus mixtes, tels ceux des agriculteurs et des travailleurs indépendants, entre revenu du travail et revenu du capital) laisse présumer que l’élasticité de substitution est effectivement unitaire.

Une deuxième caractéristique de la fonction Cobb-Douglas est son homogénéité de degré un. Cela implique l’absence d’économie d’échelle: lorsqu’on augmente de 1 p. 100 la quantité de capital et la quantité de travail utilisées conjointement, le produit augmente d’autant. Le produit dépend des quantités de facteurs entrant en combinaison, compte tenu de leurs élasticités de production respectives (mesurées par les coefficients 見 et 1 漣 見), mais non de l’échelle à laquelle les facteurs de production sont de façon conjointe mis en œuvre. Notons que cette caractéristique d’homogénéité de degré un aboutit ici, compte tenu de la substituabilité modérée des facteurs, à des conséquences moins paradoxales que celles qu’entraîne l’hypothèse de complémentarité rigide dans les relations paramétriques des modèles postkeynésiens. Si l’on double, par exemple, la quantité de capital, la quantité de travail restant constante, en l’absence de tout progrès technique, l’accroissement du produit sera nul. Avec une fonction Cobb-Douglas dans les mêmes hypothèses, si nous supposons un coefficient d’élasticité de la production égal à 0,3 pour le capital, la production s’accroîtra néanmoins de 30 p. 100.

La fonction Cobb-Douglas a été utilisée dans la construction d’un très grand nombre de modèles théoriques de croissance, ainsi que dans certains travaux de planification. Nous commencerons par présenter la première application qui en a été faite à la théorie de la croissance (Tinbergen, Econometrics , 1942). Nous évoquerons ensuite les variantes les plus notables de cette utilisation.

La fonction Cobb-Douglas permet d’étudier de façon conjointe le capital et le travail dans leurs rapports avec le produit. Les ajustements qui ont été tentés à partir de 1942 de séries chronologiques du produit global sur des fonctions Cobb-Douglas ont rendu nécessaire d’introduire un trend, révélant l’intervention du progrès technique dans la croissance.

En effet, si nous désignons comme précédemment les taux d’accroissement P⁰/P, K⁰/K, ⁰/N par p , k et n , les ajustements sur séries chronologiques d’une fonction du type précédent:

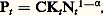compte tenu de l’hypothèse faite quant à la valeur des coefficients d’élasticité ( 廓 = 1 – 見), le calcul des taux d’accroissement révèle une tendance systématique de p à être plus grand que la somme de k et de n au cours du temps. Comme par ailleurs la fonction est homogène de degré un, ce résidu ne peut être attribué à l’intervention d’économies d’échelle.

On est ainsi conduit à introduire les effets du progrès technique sous forme d’un trend exponentiel d’accroissement de la productivité indépendamment des facteurs en quantités et en proportion, en fonction du temps, soit:

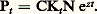Le calcul des taux d’accroissement par unité de temps donne alors:

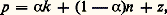z étant, de façon résiduelle, égal à la différence entre le taux de croissance de la production explicable par la variation des quantités de travail mises en œuvre, compte tenu des élasticités de production respectives des deux facteurs.

Capital et croissance

Les conclusions atteintes dans ce genre de modèle sont différentes de celles auxquelles aboutissent les modèles fondés sur l’hypothèse de complémentarité des facteurs. La contribution du capital à la croissance y paraît moins décisive. En effet, à la différence de ces modèles, où la constance de v impliquait que la productivité du capital restât constante lorsque le capital utilisé augmentait proportionnellement au travail, dans les hypothèses ci-dessus, un processus d’intensification capitalistique, c’est-à-dire une augmentation du rapport K/N, implique une diminution de la productivité du capital d’autant plus rapide à la marge (en raisonnant sur les accroissements) que le coefficient 見 a une valeur plus faible. Or la valeur de 見 se situe généralement entre 0,2 et 0,4.

En supposant la valeur de 見 égale à 0,33 et en mesurant la variation d’intensité capitalistique par k 漣 n , en l’absence de tout progrès technique, un accroissement de 1 p. 100 de K par rapport à N n’entraînera qu’un accroissement de 0,33 p. 100 du produit P. En conséquence, le coefficient de capital tendra à s’accroître. L’existence d’un trend autonome d’accroissement de la productivité est de nature à modifier cette conclusion, mais l’on démontre que ce n’est que dans le cas particulier où k 漣 n = z/ 見 que le coefficient de capital reste constant.

En revanche, en ce qui concerne le rôle éventuellement déséquilibrant joué par le capital dans le processus de croissance, la flexibilité du coefficient de capital permet d’aboutir à des conclusions plus favorables à la stabilité du processus de croissance que dans les modèles postkeynésiens.

Si, en effet, le capital varie à un taux différent de celui du produit, le coefficient de capital tendra à s’ajuster de façon à permettre la poursuite d’une croissance équilibrée. Il s’ensuit que le taux d’épargne s et le coefficient de capital v ne sont pas indépendants l’un de l’autre, à la différence des modèles postkeynésiens. Dans la même ligne de pensée, on démontre qu’en longue période (modèles dits de l’âge d’or) le taux de croissance tend à ne plus dépendre du taux d’épargne et (à population stable) à ne dépendre que du taux d’accroissement de la productivité dû au progrès technique. Le taux de croissance du produit tend à se conformer au rythme du progrès technique, et toute cause d’instabilité du processus de croissance se trouve alors éliminée.

Progrès technique et croissance

Les relations entre la croissance et le progrès technique dans le cadre de ce modèle font jouer à ce dernier un rôle prépondérant. Les effets du progrès technique sont évalués de façon résiduelle, mais le résidu ainsi dégagé représente une proportion importante du taux de croissance du produit. Si nous supposons, par exemple, que le capital s’accroît au même taux que le produit (comme ce serait la condition d’équilibre dans les modèles postkeynésiens), à supposer que la force de travail reste constante, le taux de croissance résiduelle sera, en pourcentage du taux p , équivalent à 1 漣 見. Si l’on retient pour 見 une valeur de 0,33, cela revient à calculer que les deux tiers du taux de croissance du produit, p , ne seront expliqués que, de façon résiduelle, par l’effet du progrès technique.

Compte tenu du fait que, dans les économies développées, les taux de croissance de la force de travail sont faibles et qu’en comparaison les taux de croissance du capital sont élevés, il n’est pas surprenant que, dans les mesures de ce genre, la contribution du progrès technique à la croissance représente, résiduellement, de la moitié aux deux tiers du taux de croissance global (tabl. 5).

Il est néanmoins possible d’opérer une décomposition du résidu pour faire apparaître la contribution du progrès technique à la croissance sous différentes formes: élévation du niveau d’éducation de la population, progrès scientifique, etc. (travaux de Denison, tabl. 6).

Le traitement du progrès sous forme d’un trend autonome présente, entre autres inconvénients, celui de laisser inexpliqués les mécanismes de transmission du progrès technique, qui est supposé se diffuser dans l’économie sans être, en quelque sorte, incorporé dans les facteurs de production sous forme d’une amélioration de leur qualité productive ou de leur aptitude à produire.

Les variantes du modèle

Le modèle exposé ci-dessus admet ainsi plusieurs variantes. Dans certains modèles (Solow), on fait l’hypothèse que le progrès technique transmet ses effets à la production par l’intermédiaire d’une amélioration continue de la productivité du capital, mesurée par un indice variant en fonction inverse de l’âge du capital. Chaque «génération» de capital est ainsi plus productive que la précédente. Compte tenu de la disparition progressive du capital par usure ou par obsolescence dans chaque classe d’âge et, éventuellement, de la variabilité du taux d’investissement et donc du taux d’accroissement du capital, l’effet d’un progrès technique à taux constant au moment t où l’on se place est tel que les équipements correspondant aux classes d’âge les plus récentes sont proportionnellement plus importants que le stock de capital encore en service.

Le progrès technique se trouve ainsi lié de façon complémentaire au capital, la substituabilité continuant à régir les rapports entre le capital et le travail. Ce modèle a l’inconvénient de majorer le rôle joué par le capital dans la croissance du produit, sinon directement, du moins indirectement en subordonnant tout effet du progrès technique à son incorporation dans le capital.

Il est à penser qu’une partie du progrès technique s’incorpore dans la main-d’œuvre. Il existe des variantes du modèle précédent (Phelps, «fonction à deux trends»), où seule une partie du progrès technique est supposée incorporée au capital suivant le principe précédent, un trend résiduel de progrès technique autonome subsistant par ailleurs, comme dans le modèle Tinbergen.

S’il est ainsi possible de rendre compte des mécanismes de transmission du progrès technique, les modèles de ce genre ne renseignent pas sur ses origines. L’existence du progrès technique reste une donnée exogène. Sur le plan théorique, une tentative récente d’endogénéisation est représentée par l’étude des phénomènes dits d’apprentissage (Arrow, «learning by doing »). On s’efforce alors de mesurer suivant des lois mathématiques les progrès de la productivité dus à une familiarisation croissante des managers et de la main-d’œuvre avec les techniques nouvelles de gestion ou de production.

La théorie de l’apprentissage ne peut néanmoins rendre compte que des progrès de productivité, attribuables à la main-d’œuvre, qui se manifestent à l’occasion de l’emploi de techniques nouvelles. Elle ne peut rendre compte des innovations elles-mêmes. Elle concerne le progrès du savoir-faire et non celui de la science. Cela soulève le problème de la productivité de la recherche scientifique et des ressources qui doivent lui être allouées, et dont l’utilisation n’est pas destinée à accroître directement la capacité physique de production courante. Cela soulève également le problème de la répartition des ressources entre la recherche pure, la recherche appliquée et le développement des produits et des techniques de production nouvelles.

Le problème des relations entre la croissance économique et le progrès scientifique, sous les deux aspects de la contribution de la science à la croissance et de la «production» du progrès scientifique, suggère la voie dans laquelle la théorie de la croissance, dans ses développements récents, semble devoir s’engager.

Encyclopédie Universelle. 2012.